트랜스포머 리버스 엔지니어링으로 In-context Learning 발생 이해하기
지난 4월 글에서 예상한 것처럼 Anthropic과 OpenAI 각각 두 달이 지나지 않아 대표 플래그십 모델의 뉴런 분석을 진행했는데요. 오늘은 그 연구들의 기반인, 트랜스포머 모델을 이해하려는 의미있는 시도들에 대해 알아보겠습니다.

ChatGPT는 똑똑한 만큼 답답하게 작동할 때도 많죠. LLM으로 많은 걸 할 수 있을 것 같지만, 막상 테스트를 돌려보면 간단한데도 못하는 작업들이 많습니다. 이런 일은 왜 일어날까요? 이는 LLM이 너무 사람과 닮아 있다 보니, LLM의 지능이 ‘사람과 동일한 형태의 지능’ 이라고 착각해서 문제가 발생합니다. 인공신경망은 분명히 인간의 신경망에서 영감을 받았지만, 동시에 트랜스포머는 어텐션 메커니즘이라는 완전히 다른 연산을 바탕으로 추론을 수행합니다.
트랜스포머의 작동 방식을 구성 요소에 따라 기능을 이해한다면, 우리가 하이레벨 응용에서도 의도대로 작동하는, 정확한 아이디어를 얻는 데에 유리할 텐데요. 그리고 이렇게 신경망 연산을 리버스 엔지니어링하여 분석하려는 접근 방식을 기계적 해석가능성(Mechanistic Interpretability)이라고 부릅니다. 오늘 아티클에서 이 분야가 LLM의 핵심 기능 중 하나인 In-context Learning이 트랜스포머에 어떻게 발생하는지 분석할 결과를 상변화(Phase change)와 기능 차원수(Feature dimensionality) 라는 개념을 결합하여 소개해보겠습니다.
Residual Stream
대부분 LLM의 기본이 되는 자기회기(Autoregressive) 트랜스포머의 구조를 간략히 표현하면, 먼저 토큰을 임베딩한 뒤 여러 연산을 적용하고, 마지막에 다시 텍스트로 역임베딩(un-embedding)하여 다음 토큰을 예측하는데요. 바꿔 말해 트랜스포머는 임베딩과 역임베딩 사이에서 어텐션 연산, 선형 변환 그리고 활성화 연산을 적용합니다.

여기서 잔차 흐름(residual stream)이라는 개념이 등장합니다. 잔차 흐름이란 트랜스포머에서 잔차 연결(residual connection)로 이어지는 어텐션과 활성화에 의해 업데이트되는 embedding 차원에서 벡터의 흐름을 의미하는데요. Embedding 과 un-embedding 단계 사이, 트랜스포머는 어텐션 연산과 MLP(Multi-Layer Perceptron) 연산이 반복적으로 잔차 흐름을 업데이트해 결과적으로 추론 능력을 가지게 됩니다. 이 이해의 바탕에서 트랜스포머는 유일한 벡터의 통로인 잔차 흐름을 따라 임베딩 차원이라는 메모리 대역폭 내에서 토큰 분포를 업데이트하며 최종적으로 다음 토큰을 예측합니다.
모델의 레이어가 커질수록 보틀넥의 영향은 심해지는데요. 예를 들어, 단일 레이어 트랜스포머는 잔차 흐름 차원의 4배에 해당하는 뉴런들과 통신하고, 50개의 레이어를 가지는 트랜스포머는 100배에 달하는 뉴런과 통신합니다 (동일하게 superposition hypothesis는 적용됩니다). 또한 잔차 흐름에서 대역폭을 최대한 활용하려는 수요에 기반하여 MLP 뉴런과 아래에서 설명할 어텐션 헤드 중 일부가 “메모리 관리” 역할을 수행하는 것 또한 발견되죠.
Attention head
지난 포스트에서 MLP 레이어의 활성화를 단일 의미 단위로 기능를 분리할 수 있던 것처럼, 이번에는 어텐션 레이어가 무슨 역할을 하는 지에 대하여 알아보겠습니다. 흥미롭게도, 어텐션 레이어의 개별 어텐션 헤드가 토큰 사이 정보를 이동시키고, 잔차 흐름에 독립적인 기여를 한다고 밝혀지는데요. 수학적 등치에 기반해 계산 효율성을 위해 도입된 멀티 헤드 어텐션의 개별 헤드가 각자의 역할을 수행한다는 건 짚고 넘어갈 만한 부분입니다.
Copying head
우선 어텐션 헤드의 종류 중 가장 간단한 복사 헤드(copying head) 타입부터 알아봅시다. 복사 헤드란, 말 그래도 문맥 내부에서 이전에 등장했던 토큰을복사하듯이, 비슷하거나 동일한 시퀀스에서 해당 토큰의 등장 확률을 높이는 역할을 하는데요. 어떻게 개별 어텐션 헤드가 토큰 예측에 영향을 미치는 지는, 아래에 설명할 헤드의 OV 연산에서 복사 헤드 회로의 고유값(eigenvalue)이 항상 양수라는 것으로 증명합니다.

Induction head
복사 헤드의 부분 집합인 인덕션 헤드(induction head)는 나이브한 복사 헤드같이 단순히 동일한 토큰을 복사하는 것을 넘어, 비슷한 패턴에서 특정 패턴을 완성하는 역할을 하는데요. 그리고 바로 이 인덕션 헤드의 다양한 패턴 매칭 능력이 모여 다중 레이어 트랜스포머에서 In-context learning 능력으로 발현됩니다.
복사 헤드는 단일 레이어 트랜스포머에서부터 나타나지만 In-context learning과 인덕션 헤드는 다중 레이어 트랜스포머에서만 발생하였습니다.
놀랍게도, 하나의 인덕션 헤드가 번역을 담당하는 사례도 발견되었습니다. 단일 인덕션 헤드가 단순한 작업 뿐만 아니라 복잡하거나 정교한 작업에서도 작동한다는 증거인데요. 정확히 말해서, 인덕션 헤드가 독립적으로 이전 소스 토큰에 관여(attending)하여 번역 기능이 발현됩니다.

위 그림에서 보여주는 바와 같이, 번역 인덕션 헤드의 어텐션 패턴이 어순에 따라 물결치며 따라갑니다. 구체적으로 예시 문장을 살펴 보았을 때, 영어와 프랑스어 temple이 빨갛게 하이라이팅되는 소스 토큰일 때, 추론 시점은 독일어 Tempel의 이전 토큰인 te인데요. 이는 트랜스포머가 예측을 위해 비슷한 패턴을 찾아, 이전 시점에 다음 토큰을 유도(induction)할 확률이 높이기 때문입니다.

위 테이블에서는 레이어 깊이가 40인 언어모델은 다양하게 복사 헤드와 패턴 매칭 헤드도 가지고 있다고 관측됩니다. 그렇다면 다양한 어텐션 헤드들이 내부 연산을 통해 어떻게 최종적으로 로짓(logit)에 영향을 주게 되는지, 그 과정에 대해 알아봅시다.
Mathematical approach
트랜스포머의 구조는 선형 변환과 활성화의 반복으로 대부분 이루어져 있죠. 더 단순화한다면 활성화 없이 어텐션만 가지는 트랜스포머를 수학적으로 모델링할 수 있습니다. 그렇다면 어텐션 블락을 몇 개의 행렬연산으로 간단하게 표현해, 어텐션 헤드 행렬로 어턴션 헤드가 어떻게 토큰에 관여(attending) 하는지를 수식화할 수도 있고요. 그 수학적 표현을 통해, 위에서 언급한 복사 헤드와 인덕션 헤드의 역할을 연산의 관점해서 분석해 봅시다.

어텐션 메커니즘의 4가지 가중치 행렬의 특성에 따라 QK 회로와 OV 회로, 두가지 회로(circuit)로 분리할 수 있는데요. 회로란, 신경망 안의 가중치들이 조합되어 고려될 때 신경망의 계산 상 서브 그래프(computational subgraph)를 회로(circuit)라고 부릅니다. 그리고 어텐션 헤드의 연산을 분리하면 QK 회로와 OV 회로라는 독립적인 연산으로 해석될 수 있죠. 위 그림은 하나의 인덕션 헤드가 소스 토큰(source token)과 목적 토큰(destination token) 사이 연산에 관여되는 회로를 나타냅니다.
Tensor Product representation
위 그림에서 회로 연산을 나타내는 행렬을 이해의 편의성을 위해 특정 토큰에 대한 연산만 표현했습니다. 하지만 우리는 어텐션 헤드 전체의 연산을 포괄적으로 표현하기 위해서 텐서 곱(Kronecker product) 연산자가 필요하죠. 토큰 별 벡터 연산을 종합해 어텐션 메커니즘을 아래와 같이 간단하게 표현할 수 있습니다.

위 수식을 풀어서 설명하자면, 이전 레이어의 결과값인 x에서부터 해당 레이어 결과값인 h(x)가 되는 과정이 어텐션 분포인 어텐션 패턴(attention pattern) A에 OV 가중치 행렬의 텐서곱이죠. 여기서 어텐션 패턴 A는 잔차 흐름 이전 결과값에 QK 회로를 지난 어텐션 스코어(attention score)에 소프트맥스(softmax)가 적용된 값입니다.

여기서 중요한 건 두 독립적인 회로를 따로 해석할 때 효과적이라는 점입니다. QK 행렬과 OV 행렬이 항상 같이 선형적으로 같이 연산되기 때문에 묶어서 고려될 때 추상화하여 이해에 더 편리하죠.
QK Circuit
아래와 같이 QK 회로는 얼마나 어텐션 헤드의 어텐션 패턴(attention pattern)이 계산되는 지를 나타냅니다. 이 때 QK 회로는 자기회기적이기 때문에 어텐션 패턴 계산 당시에는 붉은 색의 관여되는 토큰(attended token)이 무시되고 목적지 토큰(destination token)의 쿼리에 따라 다양하게 유사한 이전 토큰들(preceding tokens)을 고려합니다.

OV Circuit
이후에 OV 회로는 이전 토큰들 (preceding tokens)을 종합하여 어텐션 결과(attention output)에 관여하는 정도를 계산합니다. 이 연산이 의미하는 바는 패턴 매칭이 일어나서 실제 관여되는 토큰(attended token)을 해당 위치로 복사하는 실질적 역할을 수행합니다. 이 근거로, 복사 헤드의 OV 회로의 고유값(eigenvalue)이 항상 양수로 관측되고 이로 인해 토큰의 선형 조합으로 이루어진 회로가 양의 고유값으로 인해 로짓(logit) 그리고 결과적으로 해당 토큰 에 대한 확률을 상승시킵니다.

Q-Composition, K-Composition
하지만 위에서 언급했듯이, 인덕션 헤드는 단일 레이어 모델에서 발생하지 않습니다. Q-, K-합성 (composition)이라는 멀티 레이어 트랜스포머에서 레이어 사이 어텐션 헤드간 회로의 합성에서 발생하죠. 이 중 Q-, K-합성의 효과로 인한 키와 쿼리 스페이스의 변화 덕분에 단순히 복사를 넘어서 어텐션 패턴을 파악하고 더 복잡한 패턴을 완성시킬 수 있는 능력이 생깁니다.
Phase Change
위 분석이 아니더라도 In-context learning이 패턴 매칭이라는 사실은 잘 알려져 있죠. 하지만 좀 더 정확히는, in-context learning이 인덕션 헤드의 패턴 완성 능력에 의해 발생하고, 그 인덕션는 헤드는 여러 헤드의 회로상 상호작용에서 일어납니다. 그리고 단일 레이어 트랜스포머에서는 그 능력이 발현되지 않는데요. 그렇다면 학습 도중 인덕션 헤드가 어떻게 생겨날까요? 놀랍게도 이는 특정 기간에 의존적으로 발생합니다.

위 도식에서는 학습이 진행되며 특정 구간 내에서 인덕션 헤드가 늘어남과 동시에 in-context learning 점수가 증가하는 것을 보여 줍니다. 동시에 In-context learning 점수가 손실(loss)에 바로 직결된다는 점을 증명하죠. 모델이 학습될 때 손실 곡선에서 유일하게 컨벡스(convex)가 아닌 지점이 바로 이 in-context learning 능력이 향상될 때와 정확히 일치합니다! 그리고 이 지점을 상변화(Phase Change) 구간이라고 부릅니다.

Feature Dimensionality
잠깐 이전 포스트에서 다룬 신경망의 기능(feature) 이야기로 돌아가 봅시다. 우리는 신경망이 여러 중첩(superposition)되어 있는 기능의 조합으로 작동한 다는 것을 알고 있습니다. 아래 그림은 2개씩 연관된 기능(correlated feature) 4개를 2개의 평면 차원에 학습시켜 강제로 기능을 중첩시킨 예시인데요. 여기서 이 기능의 수를 3쌍으로 늘리면 맨 아래와 같이 6각형으로 연관도에 따라 배치됩니다. 이렇게 기능을 차원이 공유한다는 이해를 바탕으로 하나의 차원을 못쓰는 기능이 차원의 일부를 얼마나 차지하는지를 기능 차원수(Feature Dimensionality)로 수치화하여 정의할 수 있습니다.

그런데 이 기능 차원수(Feature Dimesnionality)가 위에서 말한 상변화(Phase Change)와 무슨 상관일까요? 소름돋는 건 모델이 학습되면서 얻는 기능들이 차원에 분배되는 상변화가 발생한다는 사실입니다.
Loss & Phase Change
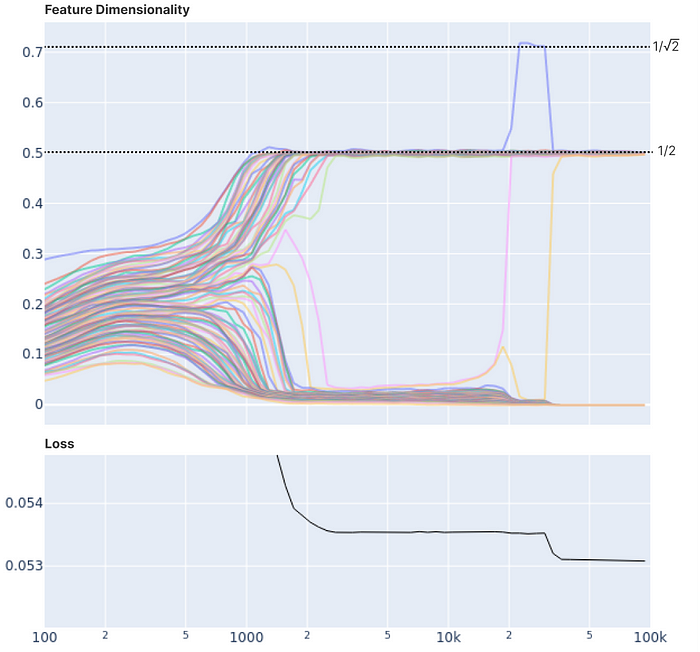
위 그래프는 임의로 초기화된 가중치가 학습되는 과정을 보여주는데요. 그런데 각각의 기능들이 학습하면서 즉 손실이 줄어들면서 동시에 기능들의 기능 차원수(Feature Dimensionality)가 하나로 수렴합니다. 즉 손실의 유의미한 변화가 기능 차원수(Feature Dimensionality)의 수렴과 함께 일어납니다. 이는 효율을 위해 기능이 각각의 차원으로 적절하게 분배된다고 이해할 수 있는데, 이 과정은 흥미롭게도 에너지 레벨 도약(energy level jump)와 유사하게 작동합니다.

이는 위 손실 곡선 시각화에서 더 명확하게 확인할 수 있는데요. 학습 과정을 보여주는 손실 곡선이 기능의 가중치 경로를 통해 동시에 일어나는 변화를 보여주고 있습니다.
위 두가지 기능 차원수(Feature Dimensionality)의 수렴으로 인한 상변화와 인덕션 헤드로 인한 상변화(Phase change)의 관계가 직접적으로 밝혀지진 않았지만, 여러 논문을 통해 분명히 유사성을 확인할 수 있습니다. 더불어, 여기서 Anthropic이 검증하고 강조한 바는 단일 의미의 차원에서 다중 의미의 뉴런으로 변화함에 따라, 뉴런의 희소성(sparsity)이 증가한다는 사실인데요. 이전 포스트에서 설명한 것과 같이 이 희소성이 주는 이점과 두 상변화 사이의 깊은 연관성으로 추측해 보건데, 학습 과정 중 상변화가 모델 그로킹(Grokking)의 핵심 요소임을 알 수 있습니다.
Pretraining & Finetuning
이런 개념적 이해를 바탕으로 기존의 사전 학습(pre tranining)과 미세 조정(fine tuning)의 애매한 정의를 공학적으로 정확하게 재정의해보는 건 어떨까요? 사전 학습을 Mechanistic Interpretability관점에서 정의한다면, 인공싱경망이 추상화된 기능을 데이터에서 추출하여 각 뉴런에 분배하는 과정이라고 합리적으로 추상화할 수 있겠네요. 언어 모델의 경우 대량의 언어 데이터를 통해 모델에 기능이 분배되며 데이터에 대한 이해를 기능으로 구축합니다.
미세 조정(fine tuning)은 뉴런에 분배되어 있는 기능의 강도를 입맛에 맞게 조절하는 것으로 볼 수 있는데요. 이미 데이터에 이해 모델이 완성된 상태이기 때문에, 어떻게 이 파라미터를 조절해야 선하거나 악한 AI, 혹은 특정 작업에 최적화된 모델을 만들 수 있습니다. 언어모델에서는 instruction tuning으로 채팅 모델을 구축하거나, 답변 선호를 최적화하는 과정이 속합니다. 이들도 세부적으로는 정의하자면 해당 기능 벡터(feature vector) 차원의 활성화를 잘 조절하는 것을 선호 최적화(preference optimization)라고 한다면, 채팅 모델과 같이 적업 최적화(task optimization)를 위한 instruction tuning은 기능 벡터(feature vector)에서 항시 활성화되어야할 차원을 고정시켜두는 작업으로 볼 수 있습니다. 또한, 어텐션 기반의 모델의 경우 사전 학습은 인덕션 헤드의 생성과 in-context learning 능력의 발생을 포함합니다.
Conclusion
다양한 분석을 통해 우리는 상변화가 다양한 레벨에서 트랜스포머 모델의 성능을 향상시킨다는 것을 알아냈습니다. 구체적으로, 인덕션 헤드와 in-context learning은 트랜스포머의 어텐션 블락을 분석해냈고 단일 의미와 기능 차원수(Feature Dimensitonality)는 트랜스포머의 MLP 레이어를 분석해냈죠. 상변화 과정은 기능 차원수가 MLP 활성화 차원에 분배되는 것을 포함했고, 어텐션 블락에서는 인덕션 헤드의 생성으로 In-context learning의 일반화 능력을 생기게 했습니다. 심지어는 더 넓은 관점에서, 일부 연구는 상변화를 거대 언어 모델 능력의 그로킹의 시점으로 연관짓고 있습니다.
무언가를 이해한다는 건 개념적으로 일반화된 작동을 이해하는 탑다운(top-down) 방식 그리고 그 구조를 하나하나 분해하여 얻는 지식인 바텀업(bottom-up) 방식이 있다고 생각합니다. 둘 중에서 한 방식에만 의존하기보다는 양 쪽 관점에서 모두 경험이 있을 때 그 분야를 더 효율적으로 정밀한 이해에 다다른다고 저는 믿는데요.
우리는 트랜스포머를 다양한 레벨에서 접근하면서, 인공지능에 대한 깊은 이해를 얻어가고 있습니다. 인덕션 헤드에 대한 연구 기여와 인덕션 헤드를 통한 in-context learning은 일종의 바텀업 방식인데요. 마찬가지로, MLP 활성화를 기능 벡터로 분해하여 단일 의미의 기능을 얻어낸 최근 연구 또한 그런 맥락의 연구입니다. 이는 LLM에 대한 바텀업 방식의 연구가 최근 몇년간 빠르게 진행되고 있음을 보여줍니다.

스페이스 오디세이 2001에서 데이빗이 HAL 9000에게 그랬던 것처럼 또는 제가 AI의 성능을 향상시키기 위해 LLM 연구를 했을 때 마주한 문제처럼 인공지능을 잘못 이해하면 모델은 기대와 다르게 행동합니다. 의도대로 인공지능을 다루고 싶다는 점에서, 그리고 안전하게 인공지능을 사용하고 싶다는 점에서 해석 가능한 인공지능(Interpretable AI)은 인공지능 정렬 (AI Alignment)에서 핵심인 분야입니다. OpenAI와 Anthropic이 이 분야를 앞다투어 연구하는 이유도 트랜스포머 내부를 이해하는 것이 지금 AI 산업의 선두가 되는 것에 중요하기 때문입니다. 최근 Sonnet이 GPT4의 성능을 앞지른 것이 최근 Anthropic의 Sonnet의 내부 뉴런 기능 분석을 진행한 것과 무관하다고 저는 생각하지 않습니다. 이처럼 트랜스포머에 대한 깊은 이해는 곧바로 그 성능에 영향을 미치기 때문에 비영리 단체와 오픈소스 진영 또한 트랜스포머 내부 작동에서 인사이트를 얻을 것으로 예상합니다. 앞으로 많은 인공지능 응용에 대한 아이디어는 물론이고, 모델 설계 개선도 해석 가능성(interpretability)에 기반하여 제안될 것을 기대합니다.
마지막으로 글의 대부분이 Anthropic, LessWrong, 그리고 OpenAI의 연구에서 따왔고, 해당 커뮤니티에 감사를 전합니다. 저는 해석 가능한 인공지능(Interpretable AI) 커뮤니티에서 발전하고 있는 기계적 해석 가능성(Mechanistic Interpretability)에 대해 알리려 노력하고 있습니다. 운이 좋게도 올해 9월부터 런던에 있는 UCL 인공지능 석사 과정에 합격하여, 앞으로 더 다양한 글을 써볼 기회가 있을 것 같습니다. 이번 글은 생각보다 길어졌지만 다음 화에는 대형 언어 모델들의 기능 분석과 최근 OpenAI가 발표한 오픈소스 도구 TDB(Transformer Debugger)에 대해 더 흥미롭게 다뤄보겠습니다.
References
아래 세가지 논문에서 내용을 발췌하여 엮었습니다.
