Reversing Transformer to understand In-context Learning with Phase change & Feature dimensionality
ChatGPT is as smart as it is frustrating at times. Let’s analyze the reasons, continuing from the previous post.
While insights suggest that LLMs can perform perfectly on some simple tasks, they often fail to answer even questions that are straightforward for humans. Why does this happen? This often stems from mistakenly equating LLM’s intelligence, which is fundamentally different, with human intelligence. Although transformers are indeed modeled after human neural networks, they operate on a completely different basic computing block called the attention mechanism.
If we separate the components of the transformer and understand the computations on a functional basis, we can gain more accurate insights for high-level applications. This approach to analyzing and reverse engineering the computing of neural networks is referred to as Mechanistic Interpretability. I will discuss how Anthropic AI has interpreted the core function of in-context learning in LLMs, which emerges from the attention mechanism, while also considering concepts like Phase change and Feature dimensionality.
Residual Stream
The basic structure of an Autoregressive Transformer involves initially embedding tokens and finally applying unembedding to perform next token prediction. In between, Attention mechanism and MLP activation occur.

The concept of a “residual stream” appears here. In a transformer, a residual stream refers to the flow of embeddings updated by the output of Attention block to residual connections. Essentially, between the embedding and unembedding stages, the transformer’s computing core, the Residual Stream, is repeatedly updated by Attention and MLP operations. Based on this understanding, the Transformer selects the next token within the memory bandwidth of the residual stream defined by the embedding dimensions, following the sole path of operations.
The larger the model’s layers, the more severe this bottleneck becomes. For example, at layer 25 of a 50 layer transformer, the residual stream contains 100 times more neurons than it has dimensions, trying to communicate with 100 times as many neurons. Perhaps due to this high demand on residual stream bandwidth, we have observed that some MLP neurons and attention heads may perform a kind of “memory management” role.
Attention head
In the last post, we discussed how MLP layers can be decomposed into mono-semantic features. This time, we’ll mainly explore the role of the Attention layer. Intriguingly, it has been discovered that individual attention heads in the Attention layer independently contribute to the residual stream mentioned above. It is impressive that each head in the multi-head attention, introduced for computational efficiency and mathematical equivalence, serves a distinct role, each presenting separate processing of information.
Copying head
Among the Attention heads, a type functioning similarly called the “copying head” has been identified. As the name suggests, a copying head increases the probability of previously appeared tokens within the context. This makes it possible for the attention head to attend to tokens based on what happened before them. How individual attention heads perform this copying function will be explained later through the positive eigenvalues of the copying matrix within the attention head.

Induction head
A subset of the copying head, the induction head, goes beyond simply copying tokens. Instead, it plays a role in completing patterns when similar representations are detected. Anthropic has precisely argued that numerous pattern matching events by induction heads lead to the emergence of in-context learning ability in multi-layer transformers.
In-context learning and induction heads manifest only in multi-layer transformers while the basic copying head appears in single-layer transformers.

Intriguingly, induction heads capable of performing translations have been identified. For instance, when the source token is ‘temple,’ the highlighted token is the one before the German ‘Tempel.’ This is because the pattern found in the translation increases the probability of inducing the next token. In relatively large models, it has been demonstrated that such patterns in sophisticated tasks like translation are also encompassed by the abilities of induction heads in the same manner.

This observation was made in a 40-layer language model, where the translation head operates alongside the copying and pattern-matching heads. Then, let’s delve deeper into the internal computing process that ultimately influences logits.
Mathematical approach
Analyzing the internal mechanisms of the copying head and the attention head could aid in understanding how they fulfill their roles. The structure of a Transformer is predominantly composed of relatively simple linear transformations and a number of activation functions. We can reduce the attention mechanism to a handful of matrix operations. Let’s mathematically express the computations of an induction head using the attention head matrix to attend to a token.

The diagram represents the circuit involved when a single induction head in a single-layer transformer computes the source and destination tokens. If we split the four weight parameters of the attention mechanism into two circuits, QK circuit and OV circuit. Here, a circuit, simply put, is when the weights within a neural network are combined and considered — it’s called a computational subgraph of a neural network. Anthropic has shown that the operations of an attention head can be interpreted as independent computations by these QK and OV circuits for the following reasons.
Tensor Product representation
The equation representing the circuit above is expressed in matrix multiplication for ease of understanding specific tokens. We can represent the entire operation of an attention head generally and simply by using a Tensor Product (Kronecker product) to perform vector per token operations, equivalent to the computing of the Attention mechanism.

We can easily express attention head operation h(x), which is the result of the previous layer x, as h(x) by tensor product the Value Weight and the Output-Value Weight matrix with the Attention Value.

Even when considering all Attention heads simultaneously, they can be expressed in the same form. The key here is that the QK circuit always operates together to compute the attention value, and the OV circuit operates together as well. Additionally, the QK circuit operates autoregressively, meaning the attended token is only ignored when calculating the attention pattern.
QK Circuit
The QK circuit computes the attention pattern for each attention head, essentially performing pattern matching.

OV Circuit
After pattern matching occurs, the OV circuit plays a role in copying the actual token to its position, as mathematically demonstrated by the positive eigenvalues of the copying matrix in the OV circuit within the attention head.

Q-Composition, K-Composition
However, as mentioned earlier, induction heads do not occur in a one-layer model. Q- and K-composition in a multi-layer transformer involve multiple layers of matrix combinations between attention heads. This Q- and K-composition not only facilitates simple copying but also affects the attention pattern, allowing attention heads to express much more complex patterns which emerge in induction heads.
Phase Change
It is well known that in-context learning fundamentally involves pattern matching. According to low-level causal research, in-context learning occurs as induction heads complete patterns. These induction heads arise from interactions within a circuit composed of multiple heads, which in single-layer models, does not manifest this capability. Then, how do induction heads develop during training? Surprisingly, the development of induction heads during training depends on a specific period in the learning process.

As learning progresses, the number of induction heads increases during a specific period, coinciding with a rise in the in-context learning score as illustrated in the above figure. Notably, this in-context learning score is directly correlated with the loss. The sole non-convex point on the curve occurs during the training of a language model, precisely when the capability for in-context learning enhances, as depicted in the figure below.

Feature Dimensionality
Let’s recall the neural network feature that was mentioned in a previous post. We know that neural networks operate as a combination of multiple superposed features. The figure below illustrates an example where four correlated features, grouped in pairs, are forced into superposition in two dimensions. If this is increased to three pairs, it results in a hexagonal arrangement at the bottom, organized according to their correlation. Here, since features share dimensions, we can mathematically define the fraction of dimension occupied by a feature as feature dimensionality.

What does feature dimensionality have to do with the phase change mentioned earlier? It is astonishing to note that as the model is trained and features are distributed across dimensions, a phase change also occurs, accompanied by a change in the loss curve.
Loss & Phase Change
The graph below illustrates the training process of weights that were initially randomized. As the training progresses and each feature reduces the loss, they tend to converge towards the same feature dimensionality. This can be understood as features being efficiently distributed across different dimensions, similar to an energy level jump.
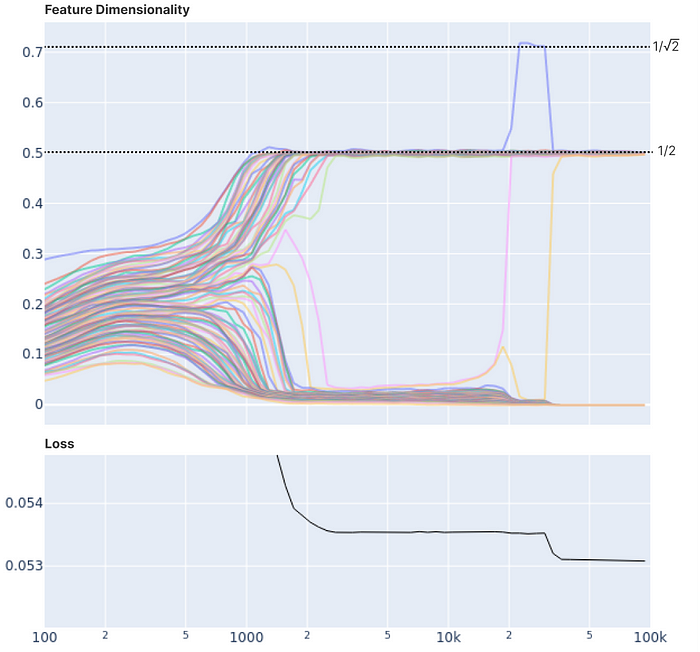
It is observable that changes in loss coincide with the convergence of feature dimensionality. Additionally, the visualization below more clearly confirms this by linking the traditional loss curve, which represents the training steps, with the trajectory of feature weights to show the simultaneous changes.

Although a direct link between the phase change in feature dimensionality and the phase change in induction heads has not been explicitly proven, what Anthropic has validated is crucial: the most important aspect to focus on is the shift from mono-semantic to poly-semantic neurons as sparsity increases, which occurs concurrently with the phase change. However, the fact that the training process involves grokking and gaining generalization capabilities allows us to speculate a deep association or even a direct causal relationship between the two.
Pre-training & Fine-tuning
Given this understanding, how about we redefine the somewhat ambiguous definitions of Pre-training and Fine-tuning more precisely from an engineering perspective? If we define training from the perspective of interpretability, it can be described as the process by which artificial neural networks extract features from data and abstract separation in each neuron.
Pre-training involves abstracting each feature in terms of dimensionality, separating them, and distributing them across neurons. It can be viewed as the LLM constructing a world model through the method of feature distribution via language.
Fine-tuning, then, can be viewed as adjusting the intensity of the features distributed across neurons to one’s liking. Since a model of the world is already completed, this involves adjusting parameters to create models that are either benevolent or malevolent AIs or are optimized for specific tasks. Common processes such as instruction tuning or creating a chat model might fall into this category. If we classify more specifically, adjusting the activation of specific feature vectors could be termed preference optimization, while fixing certain features to be always active in tasks like instruction tuning or chat models can be considered task optimization.
In the case of Attention-based models, pre-training may involve creating an induction head with emerging in-context learning and fine-tuning. Furthermore, I have to mention again that the definitions provided here are based on my abstract categorization and have not been rigorously validated.
Conclusion
Through various analyses, we have discovered that phase changes enhance the performance of language models in a different context. More specifically, the induction head and in-context learning focus on the Attention Layer and feature dimensionality are centered on the MLP layer. The phase change process involves distributing features across dimensions, and at the Attention level, the generalization capabilities created as In-context learning through the emergence of induction heads. From a broader perspective, another study has linked these critical training phase changes in LLM ability with Grokking as a point of deep relativity.
To study and understand something, there are always two approaches: the Bottom-up approach and the Top-down approach. Conceptually, there is the top-down method that involves understanding generalized operations at the level of abstraction, and the bottom-up approach, which involves deconstructing the structure piece by piece or learning by actually operating it. As I studies more, relying solely on one approach over the other is less effective than having experience from both perspectives, which leads to a more precise understanding of the subject.
We need to approach the understanding of transformers at various levels, and we are enhancing the detail for alignment. The contribution of induction heads in context learning through attention heads represents a bottom-up approach. Additionally, the recent proof that MLP activation at the token level is divided into mono-semantic features, enabling analysis up to the level of GPT-2, shows that the bottom-up approach has rapidly evolved over the years.

Like when I conducted research on the QA performance of LLMs, I have encountered instances where parts did not function as expected due to overestimating the intelligence of artificial intelligence. Interpretable AI matters. The deep understanding of the internal architecture of transformers might be a key factor in OpenAI and Anthropic being at the forefront of the AI industry, which can be seen as their academic contribution. Therefore, non-commercial communities can focus on improving open-source model performance by gaining insights into the internal workings of transformers. I look forward to exploring ways to direct AI towards safe and real-world applications derived from interpretability.
Lastly, much of this article draws from research by Anthropic and LessWrong, to whom I extend my gratitude. I am attempting to simplify the explanation of a very interesting field that is evolving within these communities: Explainable AI’s Mechanistic Interpretability. Although longer than anticipated, in the next installment, I will discuss the recently released open-source tool by OpenAI, the Transformer Debugger (TDB) and Deepmind’s research about Steering vector.
Reference
Most of the content here is extracted from the following three papers, which are highly recommended for their precisely constructed experiments.
